明日は情報オリンピック本選ですね。
学校を休んで東京です。
問4.★
四角形ABCDは半径1の円に内接し,対角線どうしのなす角は60°である.対角線の交点をPとすると,AP=1/3,CP=2/3である.このときBPとDPの差の絶対値としてありうるものをすべて求めよ.ただし,XYで線分XYの長さを表わすものとする。
昨日携帯電話を買いました。最近のは多機能ですね。
解答は右下から。
(問題の著作権は数学オリンピック財団に帰属します)
<asi君の解き方>
AC=AP+CP=1/3+2/3=1
「対角線どうしのなす角は60°」について、
(i)∠APB=60°(∠CPB=120°)
(ii)∠CPB=60°(∠APB=120°)
の2つのパターンについて考える。
法べきの定理より、
BP・DP=AP・CP=1/3・2/3=2/9
求めるのは、|BP-DP|だから、
BP+DP つまり、BDさえ求めれば、
|BP-DP|2=(BP+DP)2 ‐4BP・DP
で求まる!
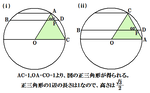
BDは半径1の円の弦の長さ。
BDの中心からの距離を求めれば弦の長さもわかる!
画像をクリックすると
鮮明に表示されます
したがって、
(i)距離:d=√3/3
(BP+DP)2=(2√1-d2)2
=4(1‐1/3)
=8/3
|BP-DP|=4/3
(i)距離:d=√3/6
(BP+DP)2=(2√1-d2)2
=4(1-1/12)
=11/3
|BP-DP|=5/3
よって、答えは 4/3,5/3 だぜ!!楽勝だぜ!
<模範解答>
ACを1辺とする正六角形を描く。
1辺1の正六角形は半径1の円に内接するので、
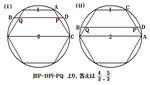
画像をクリックすると
鮮明に表示されます
なんだとっ!!!!
こんな簡単なやり方があったのか…
こっちの方が簡単だし、速いし、計算ミスする恐れもない!
完敗だ・・・
(問題の著作権は数学オリンピック財団に帰属します)
 [8回]
[8回]
PR

