問８．★★★
三角形ABCの内部に点Pがある．AP=√3，BP=5，CP=2，AB:AC=2:1，∠BAC=60°であるとき，三角形ABCの面積を求めよ．
ただし，XYで線分XYの長さを表わすものとする．

数学オリンピック予選通過の表彰状とHRで楯は貰うことにしました。
天才秀才のK君(以下ゆみおくんとする)との会話
ゆみお「中1の頃も貰ったけど、『予選通過ごときで表彰状とかなめとんのか』と思って破り捨てたわ」
asi 「ちょｗｗｗ」
asi 「楯は破れないよね」
ゆみお 「まあ、捨てるわ」
asi 「じゃちょーだい」
ゆみおは数学の合宿を狙ってます。
俺は……数学も情報もビミョー・・・

何と言っても、俺がここ何年も貫いてきた「期待しない精神」を大事にするぜ。

解答は右下から

(問題の著作権は数学オリンピック財団に帰属します)

<asiの解答>
言わずもがなだが、三角定規型だな。



　クリックすると
　　鮮明に表示されます






この3元二次方程式を気合いで解く。
面積をSとすると、S=(√3/2)c²となる。だから、c²を求めたい。
③-①：-2√3ac+3c²=21
①より、a=√(4-b²)なので、
代入して、-2√(12-3b²)c+3c²=21
変形して、3c²-21=2√(12-3b²)c
9c⁴-126c²+441=48c²-12b²c²　…④
つまり、
9c⁴-126c²+441=48c²-12(bc)²　…④
②-①：-2bc+c²=-1
よって、2bc=c²+1
④に代入して、9c⁴-126c²+441=48c²-3(c²+1)²
9c⁴-126c²+441=48c²-3c⁴-6c²-3
12c⁴-168c²+444=0
両辺12で割って、
c⁴-14c²+37=0
c²=7±2√3
c²=7-2√3 のときは矛盾が生じる
(Pが⊿ABCの外側に出来るとかだったと思う)
矛盾が出来ることを必死に証明する(ひたすら計算)
よってc²=7+2√3
∴S=(7√3+6)/2

しかし！

答案に書いた答え：(7√3-6)/2
(計算ミスしてc^2=7+2√3のとき矛盾が生じた)

何だよ俺は！
問７では問題文を読み間違い、問８では計算間違い！
こんなミスで2点も落としている！8点だったら全国3位だぞ！(予選免除者も含めたらだいぶ落ちるが)
ミスも実力のうち？ああ、そうだよ。認めるよ！
俺は単純ミスで自分の実力が落ちてるのが悔しいんだよ！
「運命を呪うぜ…」という訳にもいかないので、自分の脳みそを呪うぜ…(なんかバカっぽいセリフだな)

<模範解答>



　クリックすると
　　鮮明に表示されます







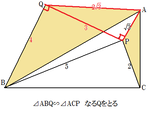
⊿ABQ∽⊿ACP なるQをとると、
相似比はAB:AC=2:1
よって、AQ=2AP=2√3,BQ=2CP=4
AQ:AP=2:1,∠QAP=60°から、⊿AQPは三角定規型
よって、PQ=3
したがって、⊿PQBは3:4:5の三角形、∠BQP=90°
∴AB²=PQ²+(AP+BQ)²=28+8√3
(∠AQB=90°+30°=120°から、⊿AQBについての余弦定理から求めてもよい)
したがって、
⊿ABC=(1/2)×AB×AC×sin60°
 =(1/2)×AB×(1/2)AB×√3/2
 =√3/8×AB^2
 =(6+7√3)/2

製作者すげ～

(問題の著作権は数学オリンピック財団に帰属します)

[1回]