今日、情報オリンピックの本選がありました。出来は……微妙。期待し過ぎるのはよくないですね。でもまあしかし思ったのは、みんなタイピング速度すごいですね。
問6.★★★
赤色の島,青色の島,黄色の島がそれぞれちょうど3つずつある.これらの島に次の条件をみたすようにいくつかの橋をかける.
●どの2つの島も,1本の橋で結ばれているか結ばれていないかのいずれかであって,橋の両端は相異なる2つの島に繋がっている.
●同色の2つの島を選ぶと,その2つの島は橋で直接結ばれておらず,その2つの島の両方と直接結ばれている島も存在しない.
橋のかけ方は何通りあるか.ただし,1本も橋をかけない場合も1通りと数える.
わかっているともいますが、3つの赤色の島、青色の島、黄色の島はそれぞれ区別します。
ですから、答えは結構大きな値になります。
解答は右下から
(問題の著作権は数学オリンピック財団に帰属します)
問題の意味を解釈しましょう。
・どの2つの島も,1本の橋で結ばれているか結ばれていないかのいずれかであって,
これは2島間に橋が2本以上架かっていない事を意味します。(図1)
・橋の両端は相異なる2つの島に繋がっている.
橋が行き止まりだったり(図2)自分の島に戻る物だったりはしない(図3)という意味です。
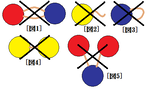
・同色の2つの島を選ぶと,その2つの島は橋で直接結ばれておらず,
(図4)という意味です。
・その2つの島の両方と直接結ばれている島も存在しない
(図5)という意味です。
クリックすると
鮮明に表示されます
ここで、赤色の島と青色の島との橋の架け方がn通りだったとします。
赤色の島と青色の島との橋の架け方は、赤色の島と黄色の島との橋の架け方や黄色の島と青色の島との橋の架け方に影響を与えず、「独立している」ので、橋の架け方は全部でn^3通りあります。
(i)2島間に橋を架けない:1[通り]
(ii)2島間に1本橋を架ける:(3C1)2×1!=9[通り]
(ii)2島間に2本橋を架ける:(3C2)2×2!=18[通り]
(ii)2島間に3本橋を架ける:(3C3)2×3!=6[通り]
∴1+9+18+6=34[通り] したがって、343=39304[通り]
もうちょっと優等生っぽく答案を書くと、
 ^{2} \times k!\right) =34) から、
から、
343=39304[通り]
(問題の著作権は数学オリンピック財団に帰属します)
 [1回]
[1回]
PR

