いよいよ決勝は明日ですね。
明日はそれで丸一日潰れるので今日中に宿題(たまった分も含め)やらにゃな~
問2.★
0以上10000以下の整数の中で,10進法で表記したときに1が現れないようなもののすべての平均を求めよ.
この調子だと決勝の問題をブログに上げるのは11日後ですかぁ
解答は右下から。
(問題の著作権は数学オリンピック財団に帰属します)
<解答>
例えば、0以上9999以下のすべて整数の平均を求めるとする。
(0+9999)/2=9999/2 だ。
もしこのやり方がわからないなら、合計から10000を割ってもいい。
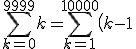 = \frac{1}{2} \left(10000 \times 10001\right) -10000)
=50005000‐10000
=49995000
これを10000でわって、9999/2
もしくは、
0+1+2+3+…+9998+9999=(0+9999)×10000/2=49995000
これを10000でわって、9999/2
いくらでも答えの出し方があるのだが、ここで用いるのは以下の考え方だ。
1の位が0となるのは、10,100,1000の位がそれぞれ10通りずつ、103=1000通り
1の位が1となるのは、10,100,1000の位がそれぞれ10通りずつ、103=1000通り
1の位が2となるのは、10,100,1000の位がそれぞれ10通りずつ、103=1000通り
同様に、全て1000通りずつ、つまり同確率で現れる。
したがって、1の位の値の合計は
(0+1+2+3+4+5+6+7+8+9)×1000=45000
同様に求めて、10の位、100の位、1000の位も値の合計は45000
したがって、0以上9999以下のすべて整数の合計は、
45000×1000+45000×100+45000×10+45000×1=49995000
これを10000で割って、9999/2
もしくは、1,10,100,1000の位の平均はすべて9/2より、
9/2×1000+9/2×100+9/2×10+9/2=9999/2
としてもよい。
計算するときは
=9/2×(1000+100+10+1)=9/2×1111
とまとめたら楽。
この考え方を使う。
10000は1を含む数なので、0以上9999以下の整数の中で、10進法で表記したときに1が現れないようなもののすべての平均を考えればよい。
1の位が0となるのは、10,100,1000の位がそれぞれ9通りずつ、93=729通り
1の位が2となるのは、10,100,1000の位がそれぞれ9通りずつ、93=729通り
1の位が3となるのは、10,100,1000の位がそれぞれ9通りずつ、93=729通り
同様に、全て729通りずつ、つまり同確率で現れる。
したがって、1の位の値の合計は
(0+2+3+4+5+6+7+8+9)×729=44×729=32076
同様に求めて、10の位、100の位、1000の位も値の合計は33891
したがって、0以上9999以下のすべて整数の合計は、
32076×1000+32076×100+32076×10+32076×1=35636436
これを94=6561で割って、48884/9
もしくは、1,10,100,1000の位の平均はすべて44/9より、
44/9×1000+44/9×100+44/9×10+44/9=48884/9
又は、 44/9×1111=48884/9
(問題の著作権は数学オリンピック財団に帰属します)
*追伸
わかっていると思うけど、
9999/2 というのは、 のことですよ。
のことですよ。
PCでは一行の方が書きやすいしね。
 [1回]
[1回]
PR

