明日は卒業式。高1は休み。
卒業式が済んだらすぐに2次試験ですね。
高3の先輩方の健闘をお祈りします。
さて、我々は明後日に決勝ですね。頑張りましょう。
問1.★
a>b>c>d>e>fを満たし,a+f=b+e=c+d=22となるような正の整数の組(a,b,c,d,e,f)はいくつあるか.
まあ、これは簡単だわな。
解答は右下から。
(問題の著作権は数学オリンピック財団に帰属します)
<解答>
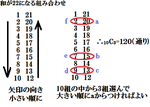
まず和が22となるような自然数の組み合わせを表にしたりするようなことが出来たら解き方の見当がつきますな。
画像をクリックすると
鮮明に表示されます
もっと優等生っぽく答案を書けば,
c>d,c+d=22 より,
2c>c+d=22 ∴c>11
2d<c+d=22 ∴d<11
よって,a>b>c>11>d>e>f となる.
0<f<e<d<11なる自然数d,e,f をとれば,
a+f=b+e=c+d=22 より,
0<22-a<22-b<22-c<11
-1を掛ければ符号が逆転するので,
0>a-22>b-22>c-22>-11
22を足して,
22>a>b>c>11
よって,a>b>c>d>e>f の条件を満たす.
したがって、0<f<e<d<11なる自然数d,e,f の取り方を求めればよい。
0<f<e<d<11なる自然数d,e,f の取り方は、
1≦f<e<d≦10 (d,e,f∈N (「d,e,f は自然数」の意))
の組み合わせなので、
10C3=120[通り]
数学オリンピックが発表している模範解答よりも詳しく書いてみた。
これでわからんやつはいまい。
(問題の著作権は数学オリンピック財団に帰属します)
 [0回]
[0回]
PR

